אוניברסליות (תורת הקטגוריות)

בתורת הקטגוריות, אוניברסליות היא תכונה של אובייקטים כלליים במסגרת קטגוריה נתונה, שממנה נובע שהם מייצגים משפחה רחבה של אובייקטים. למינוח זה שימושים רבים בתחומים שונים במתמטיקה, כמו אלגברה, טופולוגיה אלגברית ועוד. במקרים רבים ההצדקה לקיומה של בניה מתמטית היא בכך שהיא מספקת אובייקט אוניברסלי.

הגדרה פורמלית

יהיו $C,D$ קטגוריות נתונות. יהי $U:D\to C$ פונקטור ו-$X$ אובייקט של $C$.

מורפיזם התחלתי מ-$X$ ל-$U$ הוא זוג $(A,\varphi )$ כאשר $A$ אובייקט של $D$ ו-$\varphi :X\to U(A)$ מורפיזם ב-$C$, כך שמתקיימת תכונת ההתחלתיות: לכל אובייקט $Y$ ב-$D$ ולכל מורפיזם $f:X\to U(Y)$ קיים ויחיד מורפיזם $g:A\to Y$ כך ש-$U(g)\circ \varphi =f$, כלומר הדיאגרמה הבאה מתחלפת:

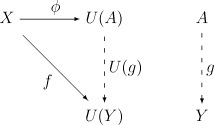
בדומה, מורפיזם סופי הוא מורפיזם דואלי לקודם: זהו אובייקט סופי מ-$U$ ל-$X$, כלומר זוג $(A,\varphi )$ כאשר $A$ אובייקט של $D$ ו-$\varphi :U(A)\to X$ מורפיזם ב-$C$, כך שמתקיימת התכונת הסופיות: לכל אובייקט $Y$ ב-$D$ ולכל מורפיזם $f:U(Y)\to X$ קיים ויחיד מורפיזם $g:Y\to A$ כך ש-$\varphi \circ U(g)=f$, כלומר:

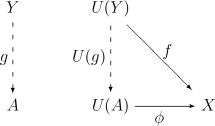
מורפיזם אוניברסלי הוא בהגדרה אחת משתי הבניות לעיל, ואוניברסליות היא אחת מהתכונות (ההתחלתית או הסופית) בהתאם. בהתאם לדואליות של המונחים, ניתן להגדיר רק אחד מהם, והשני נובע ישירות על ידי החלפת כיווני החצים.

קיום ויחידות

אם קיים אובייקט אוניברסלי, אז הוא יחיד עד כדי איזומורפיזם. זאת משום שאם A,B אוניברסליים אז יש מורפיזם יחיד מ-A ל-B, ומורפיזם יחיד מ-B ל-A, שהרכבתם (שהיא מורפיזם מ-A ל-A) מוכרחה להיות הזהות. עם זאת, לא בכל קטגוריה קיים אובייקט אוניברסלי.

דוגמאות

• מכפלה חופשית היא דוגמה לבנייה אוניברסלית בתורת החבורות, המגדירה באופן מלא את כל ההעתקות משתי חבורות נתונות לחבורה נוספת. בדומה, מכפלת היתוך היא בנייה מעט משוכללת יותר, העונה על בעיה שימושית גם בטופולוגיה אלגברית במשפט ואן קמפן.
• מכפלת חוגים היא בעלת תכונה אוניברסלית הקובעת את המיפויים מאוסף חוגים בעזרת מכפלתם. מכפלה טנזורית של אלגברות (מעל שדה) היא האלגברה הכללית ביותר המהווה תמונה של אלגברת המכפלה הקובעת את ההעתקות מהמכפלה לאלגברה אחרת.
• אלגברת קליפורד היא האלגברה הכללית ביותר בה העלאה בריבוע שקולה להפעלת תבנית ריבועית.

ראו גם

• מכפלה (תורת הקטגוריות)
• אובייקט התחלתי ואובייקט סופי
• אובייקט חופשי (תורת הקטגוריות) תבנית:אנ