אנרגיה פוטנציאלית חשמלית

תבנית:מקורות אנרגיה פוטנציאלית חשמלית היא אנרגיה פוטנציאלית האצורה בשדה חשמלי, הנובעת מכוח לורנץ הפועל על מטען חשמלי בשדה אלקטרומגנטי. ביחידות SI, אנרגיה פוטנציאלית חשמלית נמדדת בג'אול.

אנרגיה פוטנציאלית של חלקיק טעון

פוטנציאל ואנרגיה פוטנציאלית חשמלית של חלקיק טעון, כתלות במרחק ובסוג המטען.

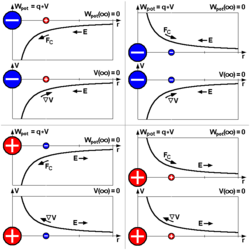
האנרגיה החשמלית נובעת מהימצאותו של מטען חשמלי בתוך שדה חשמלי. האנרגיה הפוטנציאלית החשמלית של חלקיק q המצוי בפוטנציאל חשמלי $V(r)$ שווה למכפלה $qV(r)$. העבודה הנדרשת להעברת מטען זה דרך הפרש פוטנציאלים נתונה על ידי המשוואה הבאה: $W_{ab}=q{V}_{ab}=q(V_a-V_b)$

אנרגיה פוטנציאלית האצורה בקבוצת מטענים

האנרגיה הפוטנציאלית בין שני מטענים שווה לאנרגיה הפוטנציאלית של אחד המטענים בהשפעת השדה החשמלי שיוצר חשמל של המטען השני. כלומר, אם מטען $q_1$ יוצר בנקודה $r_2$ בה מונח מטען $q_2$ פוטנציאל חשמלי $V_{r_2}$, אז האנרגיה הפוטנציאלית האצורה תהיה: $U=q_2{V}_{r_2}$. ניתן היה לחשב את האנרגיה גם על פי הפוטנציאל בנקודה $r_1$, ולכן ברור שמתקיים: $U=q_1{V}_{r_1}=q_2{V}_{r_2}=\frac{1}{2}(q_1{V}_{r_1}+q_2{V}_{r_2})$

ביטוי זה ניתן להכללה עבור קבוצה של $N$ מטענים $q_i$ הממוקמים בנקודות $r_i$, כאשר בכל אחת מנקודות אלו יש פוטנציאל של $V_{r_i}$ שנוצר בהשפעת כל המטענים פרט למטען הנמצא בנקודה $r_i$. הביטוי עבור המקרה הכללי הוא: $U=\frac{1}{2}\sum _{i=1}^N{q}_i{V}_{r_i}$

הערה: ההכפלה בחצי נועדה לפצות על ספירה כפולה של ההשפעה ההדדית בין כל שני מטענים.

אנרגיה פוטנציאלית האצורה בפילוג מטען מרחבי

ניתן להכליל שוב את הביטוי מהסעיף הקודם כדי לקבל ביטוי עבור האנרגיה הפוטנציאלית של פילוג מטען שאינו מורכב בהכרח מאוסף מטענים נקודתיים אלא מפוזר על פני מרחב:

$U=\underset{V}{\iiint }\frac{1}{2}\rho \phi dV$

כאשר:

$u$ היא צפיפות האנרגיה הנפחית.

$\rho$ היא צפיפות המטען הנפחית.

$\phi$ הוא הפוטנציאל החשמלי.

$dV$ היא יחידת נפח אינפיניטסימלית.

הצפיפות במקום ללא מטען היא 0, כך שלרוב צריך לבצע אינטגרציה על התחום בו הגוף הטעון נמצא בלבד משום שהאינטגרל מתאפס בשאר המרחב.

אנרגיה פוטנציאלית האצורה בשדה חשמלי

ניתן להשתמש במשוואה של האנרגיה הפוטנציאלית האצורה בפילוג מטען מרחבי ולהביאה למונחים של השדה החשמלי.

על פי חוק גאוס (בצורתו הדיפרנציאלית): $\mathrm{\nabla }\cdot \overrightarrow{E}=\frac{\rho }{{\epsilon }_r{\epsilon }_0}$

כאשר:

${\epsilon }_r$ הוא המקדם הדיאלקטרי היחסי של התווך.

${\epsilon }_0$ הוא המקדם הדיאלקטרי של הריק.

$\overrightarrow{E}$ הוא וקטור השדה החשמלי.

לכן מתקיים:

$U=\underset{V}{\iiint }udV=\frac{1}{2}\underset{V}{\iiint }\rho \phi dV=\frac{1}{2}\underset{V}{\iiint }{\epsilon }_r{\epsilon }_0(\mathrm{\nabla }\cdot \overrightarrow{E})\phi dV$

על פי חוקי אנליזה וקטורית:

$\mathrm{\nabla }\cdot (\overrightarrow{E}\phi )=(\mathrm{\nabla }\phi )\overrightarrow{E}+\phi (\mathrm{\nabla }\cdot \overrightarrow{E})$

ולכן:

$U=\frac{{\epsilon }_r{\epsilon }_0}{2}\underset{V}{\iiint }\mathrm{\nabla }\cdot (\overrightarrow{E}\phi )dV-\frac{{\epsilon }_r{\epsilon }_0}{2}\underset{V}{\iiint }(\mathrm{\nabla }\phi )\overrightarrow{E}dV$

תוך שימוש במשפט גאוס (משפט הדיברגנץ), קביעה שהפוטנציאל החשמלי באינסוף מתאפס ואינטגרל על כל המרחב ($V=\text{all space}$):

תבנית:משמאל לימין

כלומר אנרגיית כלל המערכת האצורה בשדה החשמלי היא:

$U=\underset{\text{all space}}{\iiint }\frac{1}{2}{\epsilon }_r{\epsilon }_0{E}^{2}dV$

מנוסחה זאת ניתן להגדיר צפיפות אנרגיה נפחית לאנרגיית המערכת, כלומר:

$u=\frac{1}{2}{\epsilon }_r{\epsilon }_0{E}^2$

אמנם ניתן להגדיר צפיפות אנרגיה גם באמצעות פילוג מטען מרחבי (ראו לעיל), אבל משיקולי נוחות ותאימות לתופעות מתחום האלקטרודינמיקה, מקובל להשתמש בנוסחה זו.

ראו גם

• אנרגיה
• אנרגיה פוטנציאלית