טיוטה:חקירת פונקציה

חקירת פונקציה ממשית היא תהליך שמתבצע על ידי אנליזה מתמטית על מנת ללמוד את מאפייניה של הפונקציה.

החקירה כוללת את השלבים הבאים (לא תמיד בסדר הזה):

1. בדיקת תחומי הגדרה.
2. בדיקת זוגיות ואי-זוגיות.
3. בדיקת ומציאת נקודות חיתוך עם הצירים.
4. תחומי עליה, ירידה ונקודות קיצון מקומיות.
5. תחומי קעירות, קמירות ונקודות פיתול.
6. אסימפטוטות - אופקיות, אנכיות ומשופעות.
7. שרטוט גרף הפונקציה.

תלמידי תארים אקדמיים מתבקשים לבצע תהליך חקירת פונקציה במהלך לימודי קורסים בנושאי חשבון דיפרנציאלי ואינטגרלי וחשבון אינפיניטסימלי.

תחומי הגדרת הפונקציה

תחומי ההגדרה של פונקציה הם תחומי ערכי הפרמטרים של הפונקציה, שבהם קיים לפונקציה ערך.

במערכת צירים דו מימדית, כאשר הפונקציה בעלת פרמטר אחד, תחום ההגדרה נקבע על פי תחומי ערכים של פרמטר זה.

תחומי עלייה, ירידה ונקודות קיצון מקומיות

נקודות קיצון מקומיות וגלובליות עבור הפונקציה cos(3πx)/x, 0.1≤x≤1.1

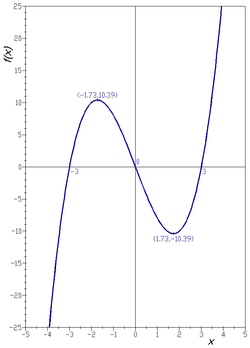
שרטוט גרף הפונקציה

דוגמה לתרשים גרף של פונקציה דו מימדית$f(x)=x^3-9x$