פונקציית איירי

במדעי הטבע, פונקציית איירי (או פונקציית איירי מהסוג הראשון) שסימונה Ai היא פונקציה מיוחדת שקרויה על שם האסטרונום הבריטי ג'ורג' בידל איירי (1801–1892). הפונקציה תבנית:משמאל לימין והפונקציה הקשורה לה תבנית:משמאל לימין, הן פתרונות בלתי תלויים ליניארית של המשוואה הדיפרנציאלית

$\frac{d^{2}y}{d{x}^2}-xy=0,$

המכונה משוואת איירי או משוואת סטוקס. זו המשוואה הליניארית הדיפרנציאלית הכי פשוטה עם נקודת מפנה (Turning Point, נקודה בה הצורה של הפתרונות משתנה מפתרון אוסילטורי מתנדנד לפתרון מעריכי).

משוואת איירי היא הפתרון של משוואת שרדינגר עבור חלקיק כלוא בתוך בור פוטנציאל קובי, או עבור חלקיק הנמצא תחת השפעת כח קבוע. מאותה הסיבה, הוא משמש גם כפתרון סמי-קלסי אחיד לקירוב ליד נקודת מפנה בקירוב WKB, כאשר הפוטנציאל ניתן לקירוב מקומי כפונקציה ליניארית של המקום.

פונקציית איירי עומדת גם בבסיס הצורה של עוצמת האור ליד ריכוז קרניים אופטיות, כמו זה של קשת. מבחינה היסטורית, זו הייתה הבעיה שהובילה את איירי לפתח את הפונקציה.

פונקציה אחרת בשם "פונקציית איירי" ממלאת תפקיד חשוב במיקרוסקופיה ובאסטרונומיה. היא מתארת את תבנית התאבכות שנוצרת על ידי מקור מעגלי נקודתי בעקבות עקיפה והתאבכות. זוהי פונקציה דו־ממדית, והיא פונקציית בסל של הרדיוס.

הגדרות

גרף. תבנית:משמאל לימין (איירי) המתכנס באדום ו-תבנית:משמאל לימין ("ביירי") המתבדר בכחול

עבור ערכים ממשיים של x, ניתן להגדיר את פונקציית איירי מהסוג הראשון על ידי אינטגרל רימן לא אמיתי:

$\mathrm{A}\mathrm{i}(x)=\frac{1}{\pi }\underset{0}{\overset{\mathrm{\infty }}{\int }}\cos (\frac{t^3}{3}+xt)dt\equiv \frac{1}{\pi }\underset{b\to \mathrm{\infty }}{\lim }\underset{0}{\overset{b}{\int }}\cos (\frac{t^3}{3}+xt)dt,$

שיתכנס כי תנודות מהירות נוטות לבטל זו את זו.

תבנית:משמאל לימין מקיימת את משוואת איירי

$y^{″}-xy=0.$

למשוואה הזו יש שני פתרונות בלתי תלויים ליניארית. עד כדי כפל בסקלר, תבנית:משמאל לימין הוא הפתרון בכפוף לתנאי תבנית:משמאל לימין כאשר תבנית:משמאל לימין. הבחירה הסטנדרטית עבור הפונקציה השנייה היא פונקציית איירי מהסוג השני, שמסומנת תבנית:משמאל לימין (מכונה לעיתים בֵּיירִי, על משקל איירי). הוא מוגדר כפתרון עם אותה משרעת תנודה כמו תבנית:משמאל לימין כאשר תבנית:משמאל לימין השונה בפאזה של π/2:

$\mathrm{B}\mathrm{i}(x)=\frac{1}{\pi }\underset{0}{\overset{\mathrm{\infty }}{\int }}[\exp (-\frac{t^3}{3}+xt)+\sin (\frac{t^3}{3}+xt)]dt.$

מאפיינים

הערכים של תבנית:משמאל לימין ו-תבנית:משמאל לימין ונגזרותיהם ב-x = 0 נתונים על ידי

$\begin{array}{cccc}\mathrm{A}\mathrm{i}(0)& =\frac{1}{3^{\frac{2}{3}}\mathrm{\Gamma }(\frac{2}{3})},& {\mathrm{A}\mathrm{i}}^{\prime }(0)& =-\frac{1}{3^{\frac{1}{3}}\mathrm{\Gamma }(\frac{1}{3})},\\ \mathrm{B}\mathrm{i}(0)& =\frac{1}{3^{\frac{1}{6}}\mathrm{\Gamma }(\frac{2}{3})},& {\mathrm{B}\mathrm{i}}^{\prime }(0)& =\frac{3^{\frac{1}{6}}}{\mathrm{\Gamma }(\frac{1}{3})}.\end{array}$

כאן, Γ, מציין את פונקציית גמא. ניתן לראות מכן שהוורונסקיאן של תבנית:משמאל לימין ו-תבנית:משמאל לימין הוא תבנית:משמאל לימין.

כאשר x הוא חיובי, תבנית:משמאל לימין היא חיובית, קמורה, ודועכת מעריכית לאפס, ו-תבנית:משמאל לימין חיובית, קמורה, וגדלה באופן מעריכי. כאשר x הוא שלילי, תבנית:משמאל לימין ו-תבנית:משמאל לימין נעים סביב אפס תדירות שעולה ומשרעת שדועכת. ניתן לראות זאת בבירור בנוסחאות האסימפטוטיות שיופיעו להלן.

פונקציות איירי מאונכות זו לזותבנית:הערה במובן שמתקיים

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{A}\mathrm{i}(t+x)\mathrm{A}\mathrm{i}(t+y)dt=\delta (x-y)$

כאשר משתמשים, שוב, באינטגרל רימן לא אמיתי.

נוסחה אסימפטוטית

פונקציית איירי Ai (בכחול), והקירוב הסינוסואידי-מעריכי עבורה (סגול)

פונקציית איירי Bi (כחול), והקירוב הסינוסואידי-מעריכי עבורה (סגול)

כפי שיוסבר להלן, ניתן להרחיב באופן אנליטי את פונקציות איירי לכל המישור המרוכב, לקבלת פונקציות שלמות. את ההתנהגות האסימפטוטית שלהן, כאשר |z| הולך לאינסוף על ערך קבוע של תבנית:משמאל לימין תלוי ב- תבנית:משמאל לימין: מה שמכונה תופעת סטוקס. עבור תבנית:משמאל לימין יש נוסחה אסימפטוטית ל-תבנית:משמאל לימין:תבנית:הערה

$\mathrm{A}\mathrm{i}(z)\sim \frac{e^{-\frac{2}{3}{z}^{\frac{3}{2}}}}{2\sqrt{\pi }{z}^{\frac{1}{4}}}\left[\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n\mathrm{\Gamma }(n+\frac{5}{6})\mathrm{\Gamma }(n+\frac{1}{6}){\left(\frac{3}{4}\right)}^n}{2\pi n!z^{3n/2}}\right].$

ואחת דומה עבור תבנית:משמאל לימין, אבל רק כאשר תבנית:משמאל לימין:

$\mathrm{B}\mathrm{i}(z)\sim \frac{e^{\frac{2}{3}{z}^{\frac{3}{2}}}}{\sqrt{\pi }{z}^{\frac{1}{4}}}\left[\sum _{n=0}^{\mathrm{\infty }}\frac{\mathrm{\Gamma }(n+\frac{5}{6})\mathrm{\Gamma }(n+\frac{1}{6}){\left(\frac{3}{4}\right)}^n}{2\pi n!z^{3n/2}}\right].$

נוסחה מדויקת יותר עבור תבנית:משמאל לימין, ונוסחה עבור תבנית:משמאל לימין כאשר תבנית:משמאל לימין או, באופן שקול, על תבנית:משמאל לימין ו-תבנית:משמאל לימין כאשר תבנית:משמאל לימין אבל לא אפס, הן:.תבנית:הערה

$\begin{array}{cc}\mathrm{A}\mathrm{i}(-z)& \sim \frac{\sin (\frac{2}{3}{z}^{\frac{3}{2}}+\frac{\pi }{4})}{\sqrt{\pi }{z}^{\frac{1}{4}}}\\ \mathrm{B}\mathrm{i}(-z)& \sim \frac{\cos (\frac{2}{3}{z}^{\frac{3}{2}}+\frac{\pi }{4})}{\sqrt{\pi }{z}^{\frac{1}{4}}}\end{array}$

כאשר תבנית:משמאל לימין, הקירובים טובים אבל אינם קירובים אסימפטוטיים מבחינה פורמלית, כי היחס בין תבנית:משמאל לימין או תבנית:משמאל לימין לקירוב לעיל מתבדר כאשר הקוסינוס או הסינוס מתאפסים. הרחבות אסימפטוטיות עבור הגבולות האלה זמינות גם כן. ניתן לראות אותן, למשל, ב-(Abramowitz and Stegun, 1954) ו-תבנית:Harv.

קלטים מרוכבים

ניתן להרחיב את ההגדרה של פונקציית איירי למישור המרוכב על ידי האינטגרל

$\mathrm{A}\mathrm{i}(z)=\frac{1}{2\pi i}\underset{C}{\int }\exp (\frac{t^3}{3}-zt)dt,$

כאשר האינטגרל הוא על מסילה $C=\{t\exp (i\pi \cdot [-\frac{1}{2}+\frac{1}{3}\frac{1-e^x}{1+e^x}]):t\in ℝ\}$, או כל מסילה שמתנהגת דומה אסימפטוטית.תבנית:הערה לחלופין, ניתן להשתמש במשוואה הדיפרנציאלית y" − xy = 0 כדי להרחיב את הפונקציות תבנית:משמאל לימין ו-תבנית:משמאל לימין להיות פונקציות שלמות במישור המרוכב.

הנוסחה האסימפטוטית של Ai עדיין בתוקף על המישור המרוכב אם לוקחים ערך מוחלט של x^2/3, ו-x אינו על הציר הממשי השלילי. הנוסחה עבור תבנית:משמאל לימין תקפה עבור x בגזרה תבנית:משמאל לימין עבור דלתא חיובית. כמו כן, הנוסחאות עבור תבנית:משמאל לימין ו-תבנית:משמאל לימין תקפות אם x הוא בתחום תבנית:משמאל לימין

מההתנהגות האסימפטוטית שלהן נובע שלשתי פונקציות איירי יש אינסוף אפסים על הציר הממשי השלילי. לפונקציה תבנית:משמאל לימין אין אפסים נוספים במישור המרוכב, בעוד שלפונקציה תבנית:משמאל לימין יש אינסוף אפסים בתחום {z ∈ C: π/3 < |arg(z)| < π/2}.

גרפים

$\mathrm{\Re }[\mathrm{A}\mathrm{i}(x+iy)]$	$\mathrm{\Im }[\mathrm{A}\mathrm{i}(x+iy)]$	$|\mathrm{A}\mathrm{i}(x+iy)|$	$\mathrm{a}\mathrm{r}\mathrm{g}[\mathrm{A}\mathrm{i}(x+iy)]$

$\mathrm{\Re }[\mathrm{B}\mathrm{i}(x+iy)]$	$\mathrm{\Im }[\mathrm{B}\mathrm{i}(x+iy)]$	$|\mathrm{B}\mathrm{i}(x+iy)|$	$\mathrm{a}\mathrm{r}\mathrm{g}[\mathrm{B}\mathrm{i}(x+iy)]$

קשרים לפונקציות מיוחדות אחרות

עבור קלטים חיוביים, פונקציות איירי מקושרות לפונקציות בסל:

$\begin{array}{cc}\mathrm{A}\mathrm{i}(x)& =\frac{1}{\pi }\sqrt{\frac{x}{3}}{K}_{\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right),\\ \mathrm{B}\mathrm{i}(x)& =\sqrt{\frac{x}{3}}(I_{\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)+I_{-\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)).\end{array}$

כאשר I ו-K הם פונקציות בסל מותאמות (modified), דהיינו, הפתרונות של משוואת בסל המותאמת

$x^2{y}^{″}+x{y}^{\prime }-(x^2+\frac{1}{9})y=0.$

הנגזרת הראשונה של פונקציית איירי היא

$\mathrm{A}{\mathrm{i}}^{\prime }(x)=-\frac{x}{\pi \sqrt{3}}{K}_{\frac{2}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)$

את הפונקציות K_1/3 ו - K_2/3 ניתן להציג עם אינטגרלים שמתכנסים במהירות.תבנית:הערה

אם הקלט (x) שלילי, ניתן לקשר בין פונקציות איירי לבין פונקציות בסל (הרגילות):

$\begin{array}{cc}\mathrm{A}\mathrm{i}(-x)& =\sqrt{\frac{x}{9}}(J_{\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)+J_{-\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)),\\ \mathrm{B}\mathrm{i}(-x)& =\sqrt{\frac{x}{3}}(J_{-\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)-J_{\frac{1}{3}}\left(\frac{2}{3}{x}^{\frac{3}{2}}\right)).\end{array}$

כאן, J_±1/3 הם פונקציות בסל, דהיינו, הן פותרות את משוואת בסל:

$x^2{y}^{″}+x{y}^{\prime }+(x^2-\frac{1}{9})y=0$.

יש גם קשר לפונקציות סקורר תבנית:אנ, תבנית:משמאל לימין שפותרות את המשוואה y" − xy = 1/π. ניתן לתאר את הפונקציות האלה בעזרת פונקציות איירי ואינטגרלים עליהן:

$\begin{array}{cc}\mathrm{G}\mathrm{i}(x)& =\mathrm{B}\mathrm{i}(x)\underset{x}{\overset{\mathrm{\infty }}{\int }}\mathrm{A}\mathrm{i}(t)dt+\mathrm{A}\mathrm{i}(x)\underset{0}{\overset{x}{\int }}\mathrm{B}\mathrm{i}(t)dt,\\ \mathrm{H}\mathrm{i}(x)& =\mathrm{B}\mathrm{i}(x)\underset{-\mathrm{\infty }}{\overset{x}{\int }}\mathrm{A}\mathrm{i}(t)dt-\mathrm{A}\mathrm{i}(x)\underset{-\mathrm{\infty }}{\overset{x}{\int }}\mathrm{B}\mathrm{i}(t)dt.\end{array}$

התמרת פורייה

בעזרת ההגדרה של פונקציית איירי, ניתן לראות באופן ישיר שהתמרת פורייה שלה היא

$ℱ(\mathrm{A}\mathrm{i})(k):=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{A}\mathrm{i}(x)e^{-2\pi ikx}dx=e^{\frac{i}{3}(2\pi k{)}^3}.$

שימושים אחרים של המונח פונקציית איירי

"פונקציית איירי" במשמעות של ההעברה של אינטרפרומטר פברי-פרו

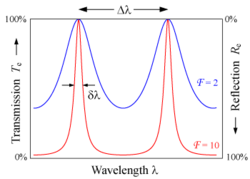
אינטרפרומטר פברי-פרו

תבנית:הפניה לערך מורחב פונקציית ההעברה של אינטרפרומטר פברי-פרו מכונה לעיתים גם היא "פונקציית איירי"תבנית:הערה

$ℱ(\mathrm{A}\mathrm{i})(k):=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{A}\mathrm{i}(x)e^{-2\pi ikx}dx=e^{\frac{i}{3}(2\pi k{)}^3}.$

כאשר לשני המשטחים יש החזרה R, ומגדירים

$F=\frac{4R}{(1-R{)}^2}$

שהוא "מקדם העידון".

עקיפה מצמצם מעגלי

"פונקציית איירי" במובן תבנית העקיפה של צמצם (חריץ) מעגלי

בלי קשר למובנים האחרים, ישנה משמעות שלישית של המונח - הצורה של דיסקת איירי, תבנית העקיפה שנוצרת מחריץ מעגלי. סוג זה של הפונקציה קשור באופן הדוק לפונקציית בסל - מדובר ב"סיבוב" של פונקציית בסל סביב הציר האנכי.

היסטוריה

פונקציית איירי קרויה על שם האסטרונום והפיזיקאי הבריטי ג'ורג' בידל איירי (1801–1892), שנתקל בה כשחקר אופטיקה (Airy, 1838). הכיתוב Ai(x) הוצג על ידי הרולד ג'פרי. איירי מונה לאסטרונום המלכותי הבריטי בשנת 1835, והחזיק במשרה עד פרישתו בשנת 1881.

לקריאה נוספת

• תבנית:Citation
• Frank William John Olver (1974). Asymptotics and Special Functions, Chapter 11. Academic Press, New York.
• תבנית:Citation;
• תבנית:Citation

קישורים חיצוניים

• תבנית:אנציקלופדיה למתמטיקה
• תבנית:MathWorld
• הדפים של הפונקציות Ai ו-Bi, באתר פונקציות וולפרם, כולל נוסחאות וגרפים.