פונקציית אקטיבציה

מבנה של נוירון מלאכותי, המציג את המיקום של פונקציית האקטיבציה לאחר הפעלת המשקלים ולפני הפלט.

פונקציית אקטיבציה לוגיסטית

פונקציית אקטיבציה או פונקציית שפעולתבנית:הערה של נוירון ברשת עצבית מלאכותית היא פונקציה מתמטית המחשבת את הפלט של הנוירון ביחס לקלטים שהוא מקבל ולמשקלם. פונקציות האקטיבציה הן מרכיב מרכזי ברשתות נוירונים, שהן צורת המימוש הנפוצה של מערכות בינה מלאכותית מודרנית. לפונקציה הנבחרת יש השפעה על ביצועי הרשת, ועל ההתאמה שלה לביצוע המשימה שעליה אומנה.

מטרת הפונקציה היא לקבוע את עוצמת הפלט של הנוירון, ביחס לקלט שקיבל. ההשראה לאופן הפעולה של פונקציות אקטיבציה התקבלה מאופן הפעולה של תאי העצב במוח, אשר הפלט שלהם נקבע בהתאם לפוטנציאל הפעולה.תבנית:הערה

נוירון ברשת נוירונים מלאכותית פועל כפרספטרון (אלגוריתם בסיסי בתחום למידת המכונה), כך שהוא מקבל וקטור קלט, מכפיל אותו בווקטור משקולות שנלמד בזמן האימון. לאחר מכן נקבע פלט הנוירון באמצעות העברת תוצאת המכפלה בפונקציית האקטיבציה.

מטרה נוספת של פונקציית האקטיבציה היא להכניס אי-ליניאריות לרשת, ולכן הפונקציות הנמצאות בשימוש רווח הן פונקציות לא ליניאריות, או פונקציות שיש בהן אלמנט כלשהו של אי ליניאריות.

פונקציית אקטיבציה לא ליניארית מאפשרת לפתור בעיות לא טריוויאליות באמצעות חיבור של מספר קטן של צמתים. פונקציות האקטיבציה המודרניות כוללות את ReLU ששימשה במודל הראייה הממוחשבת AlexNet מ-2012, את GELU ששימשה במודל BERT שאומן על ידי Google ב-2018, ואת הפונקציה הלוגיסטית סיגמואיד ששימשה במודל זיהוי דיבור משנת 2012 שפותח על ידי הינטון.

השוואה בין פונקציות אקטיבציה

מלבד הביצועים האמפיריים שלהן, לפונקציות האקטיבציה יש גם תכונות מתמטיות שונות. לכל תכונה יש השפעה כלשהי על אימון הרשת, וישנן תכונות נוספות שעשויות להשפיע עליה.

ליניאריות ואי ליניאריות

על פי משפט הקירוב האוניברסלי תבנית:אנ, רשת עצבית דו-שכבתית שמשתמשת בפונקציית אקטיבציה לא ליניארית, יכולה לקרב כל פונקציה. כאשר הנוירונים ברשת משתמשים בפונקציית אקטיבציה ליניארית, הרשת כולה שווה ערך לרשת חד-שכבתית בשל תכונות הליניאריות.

טווח

כאשר פונקציית האקטיבציה חסומה, שיטות אימון מבוססות גרדיאנט נוטות להיות יציבות יותר, מכיוון ששינוי בקלט משפיע על המשקולות באופן מוגבל בכל צעד. כאשר הפונקציה לא חסומה, האימון בדרך כלל יעיל יותר מכיוון שקלטים מסוים עשויים להשפיע בצורה חזקה יותר על השינוי במשקולות. במקרה כזה, נדרש בדרך כלל שימוש ב-learning rate תבנית:אנ קטן יותר.

פונקציות שהשיפוע שלהן באינסוף לא שואף לאפס, כלומר לא מתקיים $\underset{|v|\to \mathrm{\infty }}{\lim }|\mathrm{\nabla }f(v)|=0$, מתאימות להתמודדות עם בעיית הגרדיאנט הנעלם תבנית:אנ דוגמה לפונקציה כזו היא ReLU.

גזירות ברציפות

בשימוש בשיטות אופטימיזציה מבוססות גרדיאנט רצוי שהפונקציה תהיה גזירה ברציפות. פונקציית המדרגה (פונקציה שנותנת 0 לכל ערך שקטן מ-0, ו-1 לכל ערך שגדול מ-0) אינה גזירה ב-0, והנגזרת שלה היא 0 לכל ערך אחר, ולכן שיטות מבוססות גרדיאנט לא יכולות לבצע את השיפורים שלהם בהתבסס עליה.

פירוט מתמטי

ניתן לחלק את פונקציות האקטיבציה הנפוצות ביותר לשלוש קטגוריות: פונקציות ridge, פונקציות רדיאליות ופונקציות אגרגציה.

פונקציות ridge

השוואה בין פונקציית ReLU לבין פונקציית GELU.

פונקציות ridge תבנית:אנ הן פונקציות מרובות משתנים הפועלות על צירוף ליניארי של משתני הקלט. דוגמאות לפונקציות נפוצות הן:

• פונקציה ליניארית: $\varphi (𝐯)=a+{𝐯}^{\prime }𝐛$ ,
• פונקציית ReLU: $\varphi (𝐯)=\max (0,a+{𝐯}^{\prime }𝐛)$ ,
• פונקציית מדרגה: $\varphi (𝐯)=1_{a+{𝐯}^{\prime }𝐛>0}$ ,
• פונקציה לוגיסטית: $\varphi (𝐯)=(1+\exp (-a-{𝐯}^{\prime }𝐛){)}^{-1}$ .

ברשתות עצביות ביולוגיות, פונקציית האקטיבציה היא בדרך כלל הפשטה המייצגת את הדחף עצבי בנוירון.תבנית:הערה בצורתה הפשוטה ביותר, הפונקציה היא בינארית, כלומר הנוירון יכול לבחור האם להוציא פלט או לא. עוצמת הפלט של נוירונים חסומה, ופונקציות שמחקות את ההתנהגות הזו בצורה מהימנה הן פונקציות שהטווח שלהן הוא מרחב סופי, כמו סיגמואיד.

פונקציות רדיאליות

פונקציות רדיאליות תבנית:אנ נמצאות ברשתות מסוג RBF תבנית:אנ, שיעילות בקירוב אוניברסלי של פונקציות. פונקציה בשימוש נפוץ היא פונקציית גאוס, $\varphi (𝐯)=\exp (-\frac{\Vert 𝐯-𝐜{\Vert }^2}{2{\sigma }^2})$, כאשר $𝐜$ הוא הווקטור המייצג את מרכז הפונקציה ו-$a$ ו-$\sigma$ הם פרמטרים המשפיעים על רדיוס הגאוסיאן.

פונקציות אגרגציה

פונקציות אגרגציה תבנית:אנ נמצאות בשימוש נרחב בשכבת האגרגציה (pooling) ברשתות קונבולוציה, ובשכבת הפלט של רשתות סיווג בעלות מספר מחלקות. הפונקציות האלה מבצעות אגרגציה על הקלט, למשל בחירת הממוצע, המינימום או המקסימום. בסיווג מרובה מחלקות, נעשה שימוש בפונקציית סופטמקס שיוצרת התפלגות מהקלט שהתקבל, כלומר מייצרת וקטור שסכומו 1.

פונקציות אקטיבציה נפוצות

שם	ויזואליזציה	משוואה, $g\left(x\right)$	נגזרות, $g^{\prime }(x)$	טווח	סדר גזירות
פונקציית הזהות		$x$	$1$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^{\mathrm{\infty }}$
פונקציית מדרגה		$\{\begin{array}{cc}0& \text{if }x<0\\ 1& \text{if }x\ge 0\end{array}$	$0$	$\{0,1\}$	$C^{-1}$
טנגנס היפרבולי		$\tanh (x)\doteq \frac{e^x-e^{-x}}{e^x+e^{-x}}$	$1-g(x{)}^2$	$(-1,1)$	$C^{\mathrm{\infty }}$
ReLU תבנית:אנ		$\begin{array}{cc}(x{)}^{+}\doteq & \{\begin{array}{cc}0& \text{if }x\le 0\\ x& \text{if }x>0\end{array}\\ =& \max (0,x)=x{\mathbf{\text{1}}}_{x>0}\end{array}$	$\{\begin{array}{cc}0& \text{if }x<0\\ 1& \text{if }x>0\end{array}$	$[0,\mathrm{\infty })$	$C^0$
GELU (Gaussian Error Linear Unit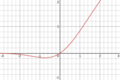)		$\begin{array}{cc}& \frac{1}{2}x(1+\text{erf}\left(\frac{x}{\sqrt{2}}\right))\\ =& x\mathrm{\Phi }(x)\end{array}$	$\mathrm{\Phi }(x)+x\varphi (x)$	$(-0.17\dots ,\mathrm{\infty })$	$C^{\mathrm{\infty }}$
Leaky ReLU		$\{\begin{array}{cc}0.01x& \text{if }x\le 0\\ x& \text{if }x>0\end{array}$	$\{\begin{array}{cc}0.01& \text{if }x<0\\ 1& \text{if }x>0\end{array}$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^0$
גאוסיאן		$e^{-x^2}$	$-2x{e}^{-x^2}$	$(0,1]$	$C^{\mathrm{\infty }}$
סופטמקס תבנית:אנ		$\frac{e^{x_i}}{\sum _{j=1}^J{e}^{x_j}}$לכל $i=1,...,j$	$g_i\left(\overrightarrow{x}\right)({\delta }_{ij}-g_j\left(\overrightarrow{x}\right))$	$(0,1)$	$C^{\mathrm{\infty }}$
Maxout		$\underset{i}{\max }{x}_i$	$\{\begin{array}{cc}1& \text{if }j=\underset{i}{\mathrm{argmax}}{x}_i\\ 0& \text{if }j\ne \underset{i}{\mathrm{argmax}}{x}_i\end{array}$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^0$

ראו גם

• פונקציה לוגיסטית